质数算法

质数打表

目标：快速列出指定范围内的所有质数。

埃氏质数筛

算法标签：数值 模拟 动态规划 打表

埃拉托斯特尼质数筛（Seive of Eratosthenes）：从第一个质数2开始在整数区间 $[2, n]$ 内进行筛选，每次筛选从区间中删除当前质数的所有倍数。筛完某个质数 $p_i$ 的倍数后，范围内的下一个未被筛除的数一定是下一个质数 $p_{i+1}$，当筛选进行到某个质数 $p_k$ 满足 $p_k^2\gt n$ 时算法结束。此后区间内所有未被筛除的数即为所有质数。

筛选质数 $p_i$ 的倍数时，可以从 $p_i^2$ 开始，不需要从 $2p_i$ 开始，因为此时从 $2p_i$ 到 $(p_i-1)p_i$ 的所有倍数都已经被小于 $p_i$ 的质数筛除。

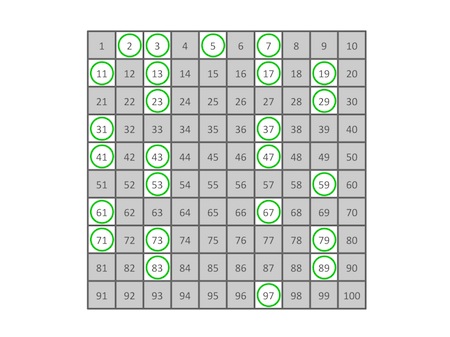
时间复杂度 $O(n\log\log{n})$，空间复杂度 $O(n)$。

缺点：当 $n\ge10^6$ 时，初期对2、3、5的倍数筛除过程耗时过长。

算法伪码

Algorithm: Seive of Eratosthenes

// $P$：逻辑值序列，即质数表；$n$：筛的上限值

$\text{EratoSeive}(P, n):$

$\ \ \ \ \ \ \ \ P\leftarrow true,P[0,1]\leftarrow false$

$\ \ \ \ \ \ \ \ p \leftarrow 2$

$\ \ \ \ \ \ \ \ \text{WHILE}\ \ p^2 \le n \ \ \text{DO}:$

$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ k\leftarrow p^2$

$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \text{WHILE}\ \ k \le n \ \ \text{DO}\ \ P[k]\leftarrow false$

$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \text{DO}\ \ p \leftarrow p+1\ \ \text{WHILE}\ \ P[p] = false$

$\ \ \ \ \ \ \ \ \text{RETURN}\ \ P$

优化：若数据规模极大，编程时尚可进行一定的优化以提高运行效率。

Tip

1. C++语言不方便将大数组初始化为全true，可采用以下方法规避：

   std::vector<bool> p(n+1, true);// 方法一：使用 vector<bool> 代替数组，直接初始化为全true
   
   bool p[MAXN+1] = { 0 }; // 方法二：反用false和true，p[k]==true 表示k为合数，false 为质数
   

2. 表中不放偶数，$P$ 的长度设置为 $n\over2$，$P[k]$ 对应 $2k+1$。

详情：埃氏质数筛

欧拉质数筛

算法标签：数值 模拟 动态规划 打表 高效率

欧拉质数筛，又叫线性筛效率比埃氏筛更高，是目前效率最高的质数打表算法：欧拉筛同样使用两层循环去筛除已知质数的倍数，但内外循环的含义和埃氏筛相反，其外循环为要筛的倍数，从2开始逐一递增，内循环为已知质数从小到大的遍历，第一个已知质数为2。这样可以避免埃氏筛初期耗时长的问题，使得整个筛选过程都比较均匀。

欧拉筛在遇到某一质数 $p$ 是倍数 $t$ 的因数，即 $t=kp,k\in\Bbb{Z}^+$ 时，这一轮筛选就立刻结束。因为对于此后的任意质数 $p^\prime\gt p$，其倍数 $tp^\prime=kpp^\prime=(kp^\prime)p$，可以留给今后的 $t^\prime=kp^\prime$ 倍数筛选循环中去。这样就可以避免埃氏筛中的重复筛除，从而达到线性筛的目标，即每一个合数都被筛除一次且仅有一次。

欧拉筛在运行时除了要有一张逻辑值表作为筛子以外，还需要额外维护一张质数表用来存放已知质数，以便内循环方便地进行遍历。当一轮外循环开始时，如果发现倍数值 $t$ 未被筛除，说明 $t$ 是一个新发现的质数，将其添加到已知质数表中。

整个筛选过程到2的倍数大于要筛选的范围上限时就完全结束了，以后不会再有合数筛除。但是和埃氏筛一样，此后会有质数余留在筛中，需要逐一检出放入已知质数表。

Example

倍数 $t$	新质数的收集	已知质数表 $P$	合数的筛除
2	2未被筛除，收集 2	[2]	2的2倍数 4
3	3未被筛除，收集 3	[2,3]	2的3倍数 6 3的3倍数 9
4	4已被筛除	[2,3]	2的4倍数 8，4能被2整除，本轮结束 3的4倍数12将留作2的6倍数去筛除
5	5未被筛除，收集 5	[2,3,5]	2的5倍数 10 3的5倍数 15 5的5倍数25大于20，本轮结束
6	6已被筛除	[2,3,5]	2的6倍数 12，6能被2整除，本轮结束 3的6倍数18将留作2的9倍数去筛除
7	7未被筛除，收集 7	[2,3,5,7]	2的7倍数 14 3的7倍数21大于20，本轮结束
8	8已被筛除	[2,3,5,7]	2的8倍数 16，8能被2整除，本轮结束
9	9已被筛除	[2,3,5,7]	2的9倍数 18 3的9倍数27大于20，本轮结束
10	10已被筛除	[2,3,5,7]	2的10倍数 20 3的10倍数30大于20，本轮结束
11	11未被筛除，收集 11	[2,3,5,7,11]	2的11倍数22大于20，本轮结束 此后不再发生合数筛除，仅收集质数
...	...	...	...
20	20已被筛除	[2,3,5,7,11,13,17,19]	结束，返回已知质数表 $P$

时间复杂度 $O(n)$，空间复杂度 $O(n)$。

缺点：使用额外空间，代码略显复杂。

算法伪码

Algorithm: Seive of Euler

// $P$：整数序列，质数表，初始为空表；$n$：筛的上限值

// $S$：逻辑值序列，即筛子；$t$：倍数；$p$：质数

$\text{EulerSeive}(P,n):$

$\ \ \ \ \ \ \ \ S[2..n]\leftarrow true$

$\ \ \ \ \ \ \ \ \text{FOR}\ \ t \leftarrow 2\ \ \text{TO}\ \ n\ \ \text{DO}:$

$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \text{IF}\ \ S[t] = true\ \ \text{TEHN}\ \ \text{Push}\ \ t\ \ \text{into}\ \ P$

$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \text{FOREACH}\ \ p\ \ \text{IN}\ \ P\ \ \text{DO}:$

$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \text{IF}\ \ t\cdot p \gt n\ \ \text{THEN}\ \ \text{BREAK}$

$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ S[t \cdot p] \leftarrow false$

$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \text{IF}\ \ p \mid t\ \ \text{THEN}\ \ \text{BREAK}$

$\ \ \ \ \ \ \ \ \text{RETURN}\ \ P$

详情：欧拉线性筛

互质算法

目标：计算整数区间 $[1,n]$ 内有序互质对的数量。

预备知识: 欧拉函数

欧拉函数 $\varphi(z):\Bbb{Z}^+\mapsto\Bbb{Z}^+$，表示在整数区间 $[1,z)$ 内有多少个数与 $z$ 互质。

$$\varphi(z)= \begin{cases} 1&,z=1\\ z\prod_{i=1}^n\left(1-{1\over{p_i}}\right)&,z\gt1 \end{cases}$$

其中 $n$ 为 $z$ 的质因数数量，$p_i$ 为 $z$ 的质因数，$i=1,\dots,n$。对照公式可直接得到计算欧拉函数的算法，从2开始一边循环寻找质因数一边迭代计算即可。

算法伪码

Algorithm: Euler's Phi Function

// $f$：质因数；$p$：函数值

$\text{Phi}(z):$

$\ \ \ \ \ \ \ \ f\leftarrow 2,p\leftarrow z$

$\ \ \ \ \ \ \ \ \text{WHILE}\ \ z \gt 1\ \ \text{DO}:$

$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \text{IF}\ \ f \mid z\ \ \text{THEN}:$

$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ p \leftarrow p - p / f$

$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \text{WHILE}\ \ f \mid z\ \ \text{DO}\ \ z\leftarrow z / p$

$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ f \leftarrow f+1$

$\ \ \ \ \ \ \ \ \text{RETURN}\ \ p$

欧拉函数的计算性质

1. 对于质数 $p$，$\varphi(p)=p-1$。
2. 若 $p$ 为质数，$n=p^k,k\in\Bbb{Z}^+$，则 $\varphi(n)=p^k-p^{k-1}$。
3. 若 $m$ 和 $n$ 互质，则 $\varphi(m\cdot n)=\varphi(m)\cdot\varphi(n)$。
4. 若 $p$ 为质数，$n=kp,k\in\Bbb{Z}^+$，则 $\varphi(n\cdot p)=\varphi(n)\cdot p$。
5. 若 $n$ 为奇数，则 $\varphi(2n)=\varphi(n)$。

欧拉函数值打表

算法标签：数值 模拟 动态规划 打表 高效率

欧拉线性筛从2开始逐个检查范围内所有整数，每一个整数被分为三种情况：1、是质数；2、是质数的倍数；3、与一质数互质。恰好对应 $\varphi$ 函数的计算性质1、4、3。因此用欧拉线性筛可以在筛出质数的同时完成 $\varphi$ 函数值的打表。

$\varphi$ 函数值必为正数，故在算法中可以将函数值表 $\Phi$ 先初始化为全0，用来代替线性筛的筛表 $S$。打表过程遇到 $\Phi(z)=0$ 即表示该整数 $z$ 为质数。此算法同时完成质数筛选和函数值打表。

时间复杂度 $O(n)$，空间复杂度 $O(n)$。

算法伪码

Algorithm: Table of Euler's Phi Function

// $P$：整数序列，质数表，初始为空表；$n$：打表的上限值

// $\Phi$：整数序列，即欧拉函数值表；$t$：倍数；$p$：质数

$\text{EulerPhiFuncTable}(P,\Phi,n):$

$\ \ \ \ \ \ \ \ \Phi[2..n] \leftarrow 0, \Phi[1] \leftarrow 1$

$\ \ \ \ \ \ \ \ \text{FOR}\ \ t \leftarrow 2\ \ \text{TO}\ \ n\ \ \text{DO}:$

$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \text{IF}\ \ \Phi[t] = 0\ \ \text{TEHN}:$

$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \text{Push}\ \ t\ \ \text{into}\ \ P\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ //$性质1

$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \Phi[t] \leftarrow t-1$

$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \text{FOREACH}\ \ p\ \ \text{IN}\ \ P\ \ \text{DO}:$

$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \text{IF}\ \ t\cdot p \gt n\ \ \text{THEN}\ \ \text{BREAK}$

$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \text{IF}\ \ p \mid t\ \ \text{THEN}:$

$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \Phi[t \cdot p] \leftarrow \Phi[t]\cdot p\ \ \ \ \ \ \ \ //$ 性质4

$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \text{BREAK}$

$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \text{ELSE}:$

$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \Phi[t \cdot p] \leftarrow \Phi[t]\cdot \Phi[p]\ \ \ \ //$ 性质3

$\ \ \ \ \ \ \ \ \text{RETURN}\ \ \Phi,P$

详情：欧拉线性筛

计算互质对数量

欧拉函数法

利用欧拉 $\varphi$ 函数值可以快速计算出 $[1,n]$ 区间内有序互质对的数量。

任一整数 $z\in [2,n]$ 在区间 $[1,n]$ 内有 $k=\varphi(z)$ 个与之互质的整数 $q_1,\dots,q_k$，则可构成 $2k$ 个有序互质对 $(q_1,n),\dots,(q_k,n),(n,q_1),\dots,(n,q_k)$。

整数1则只有它自己与自己互质，故只能构成1个互质对 $(1,1)$。

任意两个不同的整数，它们分别构成的上述有序互质对都是不同的，不会有重复。故 $[1,n]$ 区间内有序互质对的数量可用欧拉函数值表示为：

$$1+2\sum_{z=2}^n\varphi(z)$$

使用欧拉线性筛打表的方法打出 $[1,n]$ 区间上的 $\varphi$ 函数值表后，通过一次求和即可得出结果。算法伪码略。

时间复杂度 $O(n)$，空间复杂度 $O(n)$。

动态规划法

使用动态规划的方法求出 $[1,n]$ 区间内有序不互质对的数量，从总数量 $n^2$ 中减去不互质对的数量即为互质对数量。

任一整数 $z\in [2,n]$ 在区间 $[1,n]$ 内有 $\left\lfloor{n\over z}\right\rfloor$ 个倍数。任意两个倍数都有大于1的公因数 $z$，故不互质。所有倍数两两组合构成的 $\left\lfloor{n\over z}\right\rfloor^2$ 个有序数对均为不互质对。

以此方法，由不同整数构成的有序不互质对之间存在重复现象。由整数 $z$ 的倍数构造的不互质对完全包含了由 $kz,k=2,3,\dots$ 的倍数构造的不互质对，在计算时应当减去所有重复计算的部分。

使用动态规划的方法计算出由每一个整数的倍数所构造出的无重复的有序不互质对数量，计算顺序为从 $n$ 到 $2$，存放在DP备忘录 $C$ 中，递推方程为：

$$C[z]=\left\lfloor{n\over z}\right\rfloor^2-\sum_{2z\le kz\le n,k\in\Bbb{Z}}C[kz]$$

整数1和任何其他正整数都是互质的，故1不会构成不互质数对。因此上述DP过程计算完毕后即可得到问题的解，整数区间 $[1,n]$ 内的整数两两组合一共有 $n^2-\sum_{z=2}^nC[z]$ 个有序互质对。

时间复杂度 $O\bigl(nH\left(\left\lfloor{n\over2}\right\rfloor\right)\bigr)$，其中 $H(m)=1+{1\over2}+\cdots+{1\over m}$ 为调和级数的部分和，空间复杂度 $O(n)$。

算法伪码

Algorithm: Number of Coprime Pairs (DP)

// $C$：动态规划过程的DP备忘录表

// $p$：有序互质对数量

$\text{CoprimePairsDP}(n):$

$\ \ \ \ \ \ \ \ C[1] \leftarrow 0$

$\ \ \ \ \ \ \ \ \text{FOR}\ \ z \leftarrow n\ \ \text{TO}\ \ 2 \ \ \text{DO}:$

$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ C[z] \leftarrow \left\lfloor {n\over z} \right\rfloor^2$

$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ k \leftarrow 2z$

$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \text{WHILE}\ \ k \le n\ \ \text{DO}:$

$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ C[z] \leftarrow C[z] - C[k]$

$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ k \leftarrow k + z$

$\ \ \ \ \ \ \ \ p \leftarrow n^2$

$\ \ \ \ \ \ \ \ \text{FOR}\ \ z \leftarrow 2\ \ \text{TO}\ \ n \ \ \text{DO}:$

$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ p \leftarrow p - C[z]$

$\ \ \ \ \ \ \ \ \text{RETURN}\ \ p$