k位数与中位数

此处所述k位数，指一个序列中第k小的数。

给定序列 $A[0:n]$，非负整数 $0 \le k \lt n$，若对 $A[0:n]$ 进行升序排序，则k位数等于排完序后的 $A[k-1]$。

此处所述中位数，指统计意义上的中位数，即能将序列分为元素数量相等的前后两部分，使得前一部分的所有数小于等于中位数，后一部分的所有数大于等于中位数的那个数。

给定序列 $A[0:n]$，若对其进行升序排序，则中位数等于：

$$median=\begin{cases} A[k-1]&,n=2k-1\\ (A[k-1]+A[k])/2&,n=2k \end{cases},k=1,2,\dots$$

现要在不排序的条件下，以比排序更快的速度获取k位数和中位数。

序列分区

序列分区是快速排序的基本操作，可用来实现快速地k位数和中位数算法。

目标：在序列中选择一个元素作为基准，以该基准值为中心将序列分为前后两部分，前一部分所有元素小于等于基准值，后一部分所有元素大于等于基准值。

序列分区有两种常见方法，一种为基于选择的分区，中文网站和教程较为常用此方法；另一种为基于冒泡的分区，《算法导论》一书使用该方法，国外网站和教程较为常用此方法。二者都完成对子序列 $A[l:r]$ 进行分区的操作，并返回分区后基准值元素所在的位置 $p$。

基于选择的序列分区

给定子序列 $A[l:r]$，使用首元素为基准进行分区。分区时，先从右向左扫描寻找第一个小于基准值的元素，并将其交换到序列前部，然后从左到右扫描第一个大于等于基准值的元素并将其交换到序列后部，如此不断循环直到整个序列扫描完毕。

此算法在网上和算法教程中随处可见，此处不再详细描述，下面是算法的伪码。

时间复杂度 $O(n)$，空间复杂度 $O(1)$。

算法伪码

Algorithm: Partition by Selection

// $A$：待分区序列；$l, r$：子序列左右端点，左闭右开

$\text{PartitionBySelection}(A, l, r):$

$\ \ \ \ \ \ \ \ pivot \leftarrow A[l],i\leftarrow l,j\leftarrow r-1$

$\ \ \ \ \ \ \ \ \text{WHILE}\ \ i \lt j\ \ \text{DO}:$

$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \text{WHILE}\ \ i \lt j\ \ \text{and}\ \ A[j] \ge pivot\ \ \text{DO}\ \ j \leftarrow j-1$

$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \text{IF}\ \ i \lt j\ \ \text{THEN}\ \ A[i] \leftarrow A[j], i \leftarrow i+1$

$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \text{WHILE}\ \ i \lt j\ \ \text{and}\ \ A[i] \lt pivot\ \ \text{DO}\ \ i \leftarrow i+1$

$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \text{IF}\ \ i \lt j\ \ \text{THEN}\ \ A[j] \leftarrow A[i], j \leftarrow j-1$

$\ \ \ \ \ \ \ \ A[i]\leftarrow pivot$

$\ \ \ \ \ \ \ \ \text{RETURN}\ \ i$

基于冒泡的序列分区

给定子序列 $A[l:r]$，使用尾元素为基准进行分区。分区时将整个子序列分为三部分，从左到右依次为小于基准值的部分、大于基准值的部分和尚未划分的部分。初始时前两部分长度均为0，随后从左到右扫描第三部分中的每一个元素并根据其值划分到应在的部分中去。

此算法在网上和算法教程中随处可见，此处不再详细描述，下面是算法的伪码。

时间复杂度 $O(n)$，空间复杂度 $O(1)$。

算法伪码

Algorithm: Partition by Bubble

// $A$：待分区序列；$l, r$：子序列左右端点，左闭右开

$\text{PartitionByBubble}(A,l,r):$

$\ \ \ \ \ \ \ \ i\leftarrow l,last\leftarrow r-1,pivot\leftarrow A[last]$

$\ \ \ \ \ \ \ \ \text{FOR}\ \ j \leftarrow i\ \ \text{TO}\ \ last-1\ \ \text{DO}:$

$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \text{IF}\ \ A[j] \lt pivot\ \ \text{THEN}\ \ \text{Swap}(A[i],A[j]),i\leftarrow i+1$

$\ \ \ \ \ \ \ \ A[last]\leftarrow A[i]$

$\ \ \ \ \ \ \ \ A[i]\leftarrow pivot$

$\ \ \ \ \ \ \ \ \text{RETURN}\ \ i$

基于序列分区的算法

基于序列分区可以实现快速计算k位数和中位数。

分区k位数算法

目标：快速求出给定序列的k位数。

算法标签：统计 k位数 高效率 分治

利用分区的方法可以快速求出给定序列 $A[l:r]$ 的k位数，即第k小的数。k从1开始计数，1位数即序列中最小的数。此处的分区可以采用基于选择的分区方法，也可以采用基于冒泡的分区方法，二者并无区别。此处以采用基于选择的分区描述本算法。

对序列 $A[l:r]$ 进行一次分区，将序列在位置 $p_1$ 处分为 $A[l:p_1]$ 和 $A[p_1+1:r]$ 前后两个子序列。此时：

1. 若 $p_1-1 = k-1$ 则说明分区间断位置处的元素 $A[p_1]$ 即为要求的k位数；
2. 若 $p_1-1 \lt k-1$，说明k位数在后一个子序列 $A[p_1+1:n]$ 中，应递归地在此子序列中继续尝试分区；
3. 若 $p_1-1 \gt k-1$ 则说明k位数在前一个子序列 $A[0:p_1]$ 中，应在此子序列中递归尝试进一步分区。

如此递归，直至某次分区得到的间断位置 $p_i-l=k-1$，次位置处的元素 $A[p_i]$ 即为所求的k位数。此递归过程必能终止，可用循环结构完成递归。

和快速排序一样，凡是基于序列分区的算法都有平均情况和最差情况。平均情况下，每次分区的间断位置都恰在待分区序列的中间，故子问题不断减半，算法工作量的上界为：

$$W_{avg}(n)=O(n+{n\over2}+{n\over4}+\cdots+1)=O(2n-1)$$

若出现最差情况，即序列 $A[0:n]$ 本身有序，则每次分区的间断点都在头部（或尾部），于是算法退化为蛮力求解k位数的情况，工作量为：

$$W_{wst}(n)=(n-1)+(n-2)+\cdots+(n-k)=kn-\frac{k(k+1)}{2}$$

同样地，和快速排序一样，可以通过pivot随机化来规避最差情况，使得算法的平均工作量趋同为 $O(2n-1)$。

时间复杂度 $O(n)$，空间复杂度 $O(1)$。

算法伪码

kth number by partition

// $A$：原序列；$l,r$：序列左右端点；$k$：位数，$1 \le k \le r-l$

$\text{kthNumberByPartition}(A,l,r,k):$

$\ \ \ \ \ \ \ \ \text{WHILE}\ \ \text{true}\ \ \text{DO}:$

$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ pivot \leftarrow \text{Random}(l,r-1)$

$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \text{Swap}(A[l],A[pivot])$

$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ p \leftarrow \text{PartitionBySelection}(A,l,r)$

$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \text{IF}\ \ p-l = k-1\ \ \text{THEN}\ \ \text{RETURN}\ \ A[p]$

$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \text{ELSE}\ \ \text{IF}\ \ p-l \lt k-1\ \ \text{THEN}\ \ l \leftarrow p+1$

$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \text{ELSE}\ \ r \leftarrow p$

若采用基于冒泡的分区方法，则在随机选择 $pivot$ 后，应改为将其和尾部元素交换。

事实上，此算法可以不返回任何值，运行结束时k位数必为 $A[l+k-1]$。

分区中位数算法

算法标签：统计 中位数 高效率 分治

对基于分区的k位数算法进行相应改造就可以实现求中位数。

设要求中位数的序列为 $A[l:r]$，令 $n=r-l,half=\left\lfloor{n\over2}\right\rfloor$。若 $n$ 为奇数，则中位数即为排好序之后的 $A[l+half]$，即 $half+1$ 位数，只需调用上面的k位数算法取得该值即可。若 $n$ 为偶数，则中位数为排好序之后的 $(A[l+half-1]+A[l+half])/2$，即 $half$ 位数和 $half+1$ 位数的平均值，同样调用k位数算法得到 $half+1$ 位数，此后序列中 $A[l+half]$ 之前的子序列 $A[l:l+half]$ 中所有的元素值都小于等于 $A[l+half]$，所以只要在这个左半子序列中求出最大值并将其与 $A[l+half]$ 做算术平均即可得到中位数。

时间复杂度 $O(n)$，空间复杂度 $O(1)$。

算法伪码

median by partition

// $A$：原序列；$l,r$：序列左右端点

$\text{MedianByPartition}(A,l,r):$

$\ \ \ \ \ \ \ \ n\leftarrow r-l,half\leftarrow\left\lfloor{n\over2}\right\rfloor$

$\ \ \ \ \ \ \ \ median\leftarrow\text{kthNumberByPartition}(A,l,r,half+1)$

$\ \ \ \ \ \ \ \ \text{IF}\ \ n = 0 \pmod 2\ \ \text{THEN}:$

$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ max_l \leftarrow A[l]$

$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \text{FOR}\ \ i\leftarrow l+1\ \ \text{TO}\ \ l+half-1\ \ \text{DO}:$

$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ max_l \leftarrow \max(max_l, A[i])$

$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ median \leftarrow (median+max_l)/2$

$\ \ \ \ \ \ \ \ \text{RETURN}\ \ median$

缺点：基于分区的k位数算法最大的问题是时间复杂度不确定，是一个统计意义上的期望值。当k很小时，算法的时间效率可能会低于蛮力比较法。如果 $k=1$，即求最小值时，算法慢于蛮力法（蛮力法恰好进行 $n-1$ 次元素比较）。同样道理，当原序列的元素数量本身就很小时，基于分区求中位数与直接排序相比不一定更快。

锦标赛算法

算法标签：统计 锦标赛 高效率 二叉树

锦标赛算法同样用于快速求k位数、中位数，但其时间复杂度是确定的。另外，锦标赛算法也可以用于排序，时间复杂度为确定的 $O(n\log n)$。

首先模拟体育比赛中锦标赛的赛制找出最小元素：序列中的数两两分组进行比对，小者胜出进入第二轮，逐轮竞争直到最后只剩一个最小的元素胜出。这个过程可以从底向上建出一棵二叉树，树的叶子节点为序列中的元素，根节点为最小元素。称为建树过程。为了便利起见，应建立满二叉树，假设序列为 $A[0:n]$，即有 $n$ 个元素，应将元素扩展为 $2^L$ 个，其中 $L=\lceil\log n\rceil$，建完之后的满二叉树的高度为 $L+1$ 层。扩展出来的假元素（dummy）在参与竞赛的时候直接被对手淘汰。

例如下面是对序列 $A[0:7] = <4, 2, 0, 5, 9, 3, 8>$ 进行建树操作的结果：

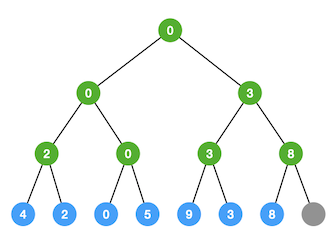
图中蓝色节点为真实的序列元素叶子节点，灰色为假元素节点，绿色为建树过程创建出的比较结果节点。比较的具体操作就是将获胜的节点复制到它的父节点上。

在叶子层上共有 $n$ 个真实的元素节点，两两分组共需进行 $\left\lceil{n\over2}\right\rceil$ 次比较，比较结果在其上一层产生 $\left\lceil{n\over2}\right\rceil$ 个有意义的节点。这一规律逐层向上是不变的，以根节点所在的层为第0层，叶子层即为第 $L$ 层，令第 $j$ 层上有意义的节点数为 $n_j$，其中 $n_0=1,n_L=n$，则该层上需要进行的两两比较次数为 $\left\lceil{n_j\over2}\right\rceil$，且有 $n_{j-1} = \left\lceil{n_j\over2}\right\rceil$。整个建树过程的工作量为 $O(n)$ 次比较。

上述建树过程结束后，最小元素已经位于根节点了，此即为1位数。若要取序列中的2位数，可以这样想，从序列中取走最小元素，再次建树后新的最小元素就是实际上的第2小元素了。而2位数一定只可能是被1位数淘汰的，且是被1位数淘汰的所有元素中最大的那个。

综上所述，若从原序列中取走最小元素，重新建树时会发生改变的只有从该最小元素的叶子节点出发向上到达树根的那条路径，别的路径上的节点不会发生任何改变。因此我们只需找到最小元素所在的叶子节点，将其改为假元素节点，然后从它开始沿着它原本的比较路径重新比较直到抵达树根即可，比较次数恰为 $L$ 次，即工作量为 $O(\log n)$。

下图为对上面建好的树进行取走1位数之后的结果，图中原先的1位数（元素0）所对应的叶子节点被改为假元素节点，然后沿着它的上升路径进行重新比较，标注为黄色节点。三次重新比较后，新的最小元素，即序列中第2小的2位数（元素2）被推上了根节点。

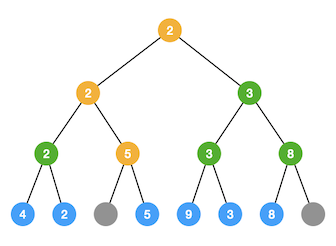
那么如果要取3位数，只需在此基础上重复上述步骤即可。如下图所示，将2位数对应的元素2的叶子节点改成假元素节点，重建图中红色的路径即可。

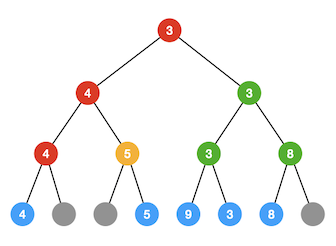
此过程可一直进行下去，每一次的工作量都是 $O(\log n)$。

若要取k位数，只要 $k-1$ 次上述操作即可，时间复杂度 $(n+k\log n)$，空间复杂度 $O(n)$。

若k等于序列长度 $n$，那么取k位数的过程相当于完成了一次排序。时间复杂度 $(n\log n)$，空间复杂度 $O(n)$。

若用于取中位数，只要根据序列长度 $n$ 的奇偶性取出合适的k位数即可。若 $n$ 为奇数，则取 $n+1\over2$ 位数即是；若 $n$ 为偶数，则中位数为 $n\over2$ 位数和 ${n\over2}+1$ 位数的平均值。

此算法在k较小时效率很高，比直接基于排序的k位数算法和基于分区的k位数算法都要快。但随着k的增大速度优势就不断减弱，当k接近中间位置时比排序取k位数要慢许多。若用于排序，比通常的其他 $O(n\log n)$ 排序算法比如快排、归并都要慢不少，因此很少见适用锦标赛排序的场景。

缺点：需使用复杂的数据结构。

最方便的用来构建锦标赛算法所需的二叉树的数据结构为顺序表存放的满二叉树。但此数据结构也并非简单结构。

另外，树的节点中除了存放元素值，还至少需要两个辅助信息：表示该节点是否位假元素的标志；元素对应的叶子节点的位置。