4.1.6. 高精算法例题:国王游戏(洛谷P1080)¶
题目描述
恰逢 \(H\) 国国庆,国王邀请 \(n\) 位大臣来玩一个有奖游戏。首先,他让每个大臣在左、右手上面分别写下一个整数,国王自己也在左、右手上各写一个整数。然后,让这 \(n\) 位大臣排成一排,国王站在队伍的最前面。排好队后,所有的大臣都会获得国王奖赏的若干金币,每位大臣获得的金币数分别是:排在该大臣前面的所有人的左手上的数的乘积除以他自己右手上的数,然后向下取整得到的结果。
国王不希望某一个大臣获得特别多的奖赏,所以他想请你帮他重新安排一下队伍的顺序,使得获得奖赏最多的大臣,所获奖赏尽可能的少。注意,国王的位置始终在队伍的最前面。
输入格式
第一行包含一个整数 \(n\),表示大臣的人数。
第二行包含两个整数 \(a\) 和 \(b\),之间用一个空格隔开,分别表示国王左手和右手上的整数。
接下来 \(n\) 行,每行包含两个整数 \(a\) 和 \(b\),之间用一个空格隔开,分别表示每个大臣左手和右手上的整数。
输出格式
一个整数,表示重新排列后的队伍中获奖赏最多的大臣所获得的金币数。
输入输出样例
输入:
3
1 1
2 3
7 4
4 6
输出:
2
说明/提示
【输入输出样例说明】
按 \(1\)、\(2\)、\(3\) 这样排列队伍,获得奖赏最多的大臣所获得金币数为 \(2\);
按 \(1\)、\(3\)、\(2\) 这样排列队伍,获得奖赏最多的大臣所获得金币数为 \(2\);
按 \(2\)、\(1\)、\(3\) 这样排列队伍,获得奖赏最多的大臣所获得金币数为 \(2\);
按 \(2\)、\(3\)、\(1\) 这样排列队伍,获得奖赏最多的大臣所获得金币数为 \(9\);
按 \(3\)、\(1\)、\(2\) 这样排列队伍,获得奖赏最多的大臣所获得金币数为 \(2\);
按 \(3\)、\(2\)、\(1\) 这样排列队伍,获得奖赏最多的大臣所获得金币数为 \(9\)。
因此,奖赏最多的大臣最少获得 \(2\) 个金币,答案输出 \(2\)。
【数据范围】
对于 \(20\%\) 的数据,有 \(1 \le n \le 10,0 \lt a,b \lt 8\);
对于 \(40\%\) 的数据,有 \(1 \le n \le 20,0 \lt a,b \lt 8\);
对于 \(60\%\) 的数据,有 \(1 \le n \le 100\);
对于 \(60\%\) 的数据,保证答案不超过 \(10^9\);
对于 \(100\%\) 的数据,有 \(1 \le n \le 1000,0 \lt a,b \lt 10000\)。
NOIP 2012 提高组 第一天 第二题
题目解析
这道题目对于初学者来说有一定的难度,涉及到一个比较隐蔽的贪心策略和一个简化版高精算法,实际编程时会遇到复杂结构、排序、STL容器等的灵活运用,代码量比较大,成员函数比较多,对编程技法也有较高的要求。
1、大臣排队的策略发现
大臣们如何排队才能满足“获得奖赏最多的大臣其所获得的奖赏尽可能少”这个要求呢?这个排队策略是比较隐蔽,不易发现的。下面我们来讨论一下怎么找出这个策略。
假如大臣数量 \(n=1\),那么没有什么排队可言,所以递推的起点为 \(n=2\)。不妨设国王左右手的数字分别为 \(a_0\) 和 \(b_0\),两位大臣为 \(p_1\) 和 \(p_2\),它们的左右手数字分别为 \(a_1,b_1\) 和 \(a_2,b_2\)。显然这时总共有两种排队方法,要么 \(p1\) 在前要么 \(p_2\) 在前:
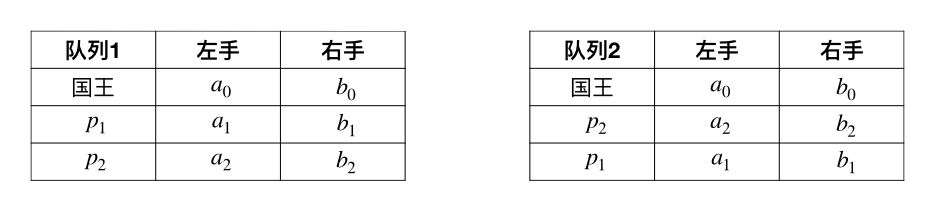
队列1:大臣 \(p_1\) 的奖赏为 \(k^1_1=a_0/b_1\),\(p_2\) 的奖赏为 \(k^1_2=a_0a_1/b_2\),奖赏最多的大臣将获得 \(K^1=\max\{k^1_1,k^1_2\}\)。
队列2:大臣 \(p_2\) 的奖赏为 \(k^2_2=a_0/b_2\),\(p_1\) 的奖赏为 \(k^2_1=a_0a_2/b_1\),奖赏最多的大臣将获得 \(K^2=\max\{k^2_2,k^2_1\}\)。
从上面的计算公式我们可以看出两个基本的不等式:\(k^1_1=a_0/b_1 \le k^2_1=a_0a_2/b_1\),\(k^2_2=a_0/b_2 \le k^1_2=a_0a_1/b_2\)。有了这两个不等式就可以继续后面的分析了。事实上纯粹用代数方法分情况讨论还是很麻烦的,为了观察方便,我们可以把已经知道的这两个数字关系标在数轴上,然后直观地进行几何意义上的分析:
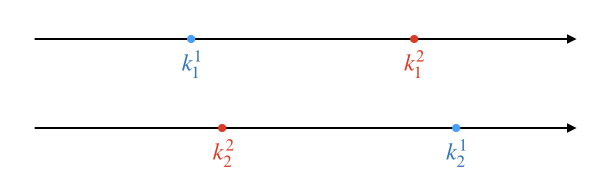
在这个图里,我把队列1时两位大臣的奖赏数点标为蓝色,队列2的两个奖赏数点标为红色。在分别的两个数轴里,我们只关心大小关系,一红一蓝两个点只要顺序不变,二者之间的距离是无所谓的。接下来我们要把两条数轴拼合到一起,由于上下两条数轴上的点相互之间的大小关系不确定,所以拼合的时候两条数轴之间可以左右移动,产生多种拼合结果,例如下面这样的各种情况:
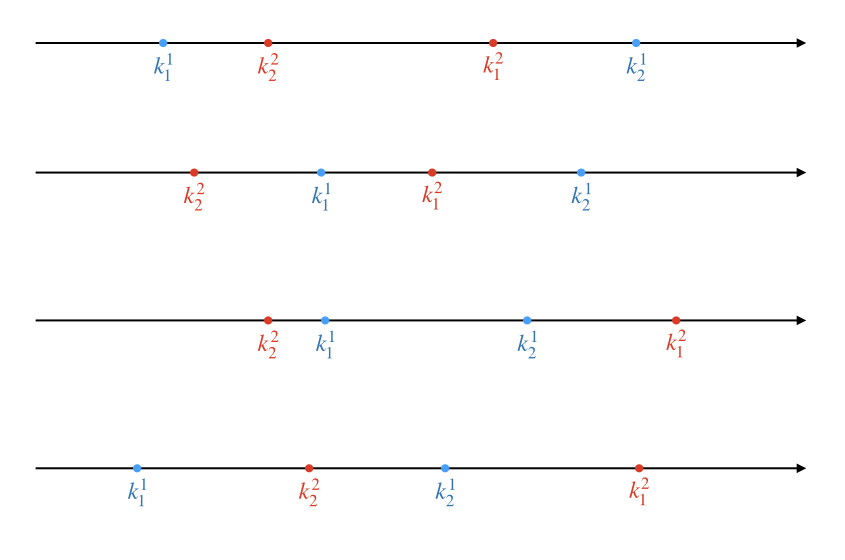
当然拼合的结果远不止这四种,还可以有很多很多种,大家可以试着画画看。但是不论怎样,我们关心的只是最右边(最大)的蓝点和最右边(最大)的红点之间的位置关系。所以我们可以发现,我们只需要关心 \(k^2_1\) 和 \(k^1_2\) 之间的大小关系。
如果 \(k^2_1 \lt k^1_2\),那么 \(k^1_2\) 就一定是最右边的点,它比两个红点都更右边,此时 \(K^1=k^1_2\) 而且一定满足 \(K^1 \gt K^2\),因此我们应该采取队列2的排法才能使得奖赏的最大值更小。把具体数字代进去我们可以得到:
\[k^2_1 \lt k^1_2 \implies \frac{a_0 \cdot a_2}{b_1} \lt \frac{a_0 \cdot a_1}{b_2} \implies a_2 \cdot b_2 \lt a_1 \cdot b_1\]换句话说,要让大臣 \(p_2\) 排在大臣 \(p_1\) 前面,就要使得它左右手数字的乘积更小:\(a_2 \cdot b_2 \lt a_1 \cdot b_1\)。
如果 \(k^2_1 \gt k^1_2\),那么 \(k^2_1\) 就一定是最右边的点,它比两个蓝点都更右边,此时 \(K^2=k^2_1\) 而且一定满足 \(K^2 \gt K^1\),因此我们应该采取队列1的排法才能使得奖赏的最大值更小。把具体数字代进去我们可以得到:
\[k^2_1 \gt k^1_2 \implies \frac{a_0 \cdot a_2}{b_1} \gt \frac{a_0 \cdot a_1}{b_2} \implies a_2 \cdot b_2 \gt a_1 \cdot b_1\]换句话说,要让大臣 \(p_1\) 排在大臣 \(p_2\) 前面,就要使得它左右手数字的乘积更小:\(a_2 \cdot b_2 \gt a_1 \cdot b_1\)。
如果 \(k^2_1 = k^1_2\),那么最右边的蓝点和红点重合,而且 \(K^1=k^1_2=k^2_1=K^2\),二者相等,取任意一种排队方法都可以,这种情况可以不用考虑。
总之,现在我们可以知道,当 \(n=2\) 时,两个大臣的排法应该是让左右手数字之积较小的那一个排在另一个前面。依此类推,我们完全有理由猜测排队的正确策略是“按照大臣左右手数字之积从小到大的顺序排队”。但是我们需要证明,证明的方法称为微扰法。
注解
这个策略是一个典型的但比较隐蔽的贪心策略,即每次都取比较简单的局部最优解,而不考虑复杂的全局最优解。如果每次的局部最优解都不会对前面已经产生的和后续将要产生的局部解产生影响,那么通过每一步都取局部最优,最后能达到全局最优。使用贪心策略来解决问题的方法叫做贪心法。使用贪心法解决问题必须证明其贪心策略的正确性,而证明贪心策略正确性的最常用方法即为微扰法。关于贪心法,在后续算法设计方法一章中会有专题讲解。
所谓微扰法,就是先假定用待证明的贪心策略生成出了一个贪心解,然后给这个解加入一点与策略不相符的最小程度的改变,称作微扰,再证明加入任意微扰后会使解变差即可证明此贪心策略的正确性。
设大臣人数为 \(n \gt 2\),已经按照“左右手数字之积从小到大”的策略排好队伍,设其中奖赏最多的大臣获得的奖赏数为 \(M\)。从游戏规则很容易看出,改变任意两个相邻大臣 \(p_i\) 和 \(p_{i+1}\) 在队伍中的顺序,并不会改变排在他们俩前面的大臣们的奖赏,也不会改变排在他们俩后面的大臣们的奖赏。现在记排在 \(p_i\) 前面的所有大臣中获得的最大奖赏数为 \(M_{1:i-1}\),如果 \(i=1\),则 \(M_{1:i-1}=0\);记排在 \(p_{i+1}\) 后面的所有大臣中获得的最大奖赏数为 \(M_{i+2:n}\),如果 \(i=n-1\),则 \(M_{i+2:n}=0\);记他们二人中奖赏较多的那个人的奖赏数为 \(M_{i:i+1}\),显然现在的全局解 \(M=\max\{M_{1:i-1},M_{i:i+1},M_{i+2:n}\}\)。
现在调换 \(p_i\) 和 \(p_{i+1}\) 的位置,用这个微扰来改变贪心解。设得到的新的解为 \(M^\prime\)。仍然以这两个大臣为界分为前中后三段,显然,排在他们俩之前的所有大臣中的最高奖赏仍然为 \(M_{1:i-1}\) 不变,排在他俩之后的所有大臣中的最高奖赏也仍然为 \(M_{i+2:n}\) 不会变。改变的仅仅是他俩中得到较高奖赏的那个人的奖赏数,我们把它记为 \(M^\prime_{i:i+1}\)。故 \(M^\prime=\max\{M_{1:i-1},M^\prime_{i:i+1},M_{i+2:n}\}\)。
现在尽管在这两个大臣可能已经不是紧挨在国王之后的了,但是我们在考虑他们两人的奖赏时,完全可以把他俩前面的所有大臣和国王进行“合体”,即把这些队伍前面的大臣左手上的数字与国王左手上的数字都乘起来,把这个乘积看作是一个“合体”后的国王左手上的数字。这样,我们前面针对 \(n=2\) 情形的结论完全适用于大臣 \(p_i\) 和 \(p_{i+1}\) 的情况,\(M_{i:i+1} \le M^\prime_{i:i+1}\) 恒成立。
那么,虽然贪心解 \(M=\max\{M_{1:i-1},M_{i:i+1},M_{i+2:n}\}\) 有可能等于 \(M_{1:i-1}\)、\(M_{i:i+1}\)、\(M_{i+2:n}\) 中的任一个,加入微扰后得到的解 \(M^\prime=\max\{M_{1:i-1},M^\prime_{i:i+1},M_{i+2:n}\}\) 同样也可能等于 \(M_{1:i-1}\)、\(M^\prime_{i:i+1}\)、\(M_{i+2:n}\) 中的任一个,但无论如何,一定成立着这样的关系:\(M \le M^\prime\)。
结论:对贪心解引入任意逆序微扰都有可能使得全局解的值增大。“按照大臣左右手上数字之积从小到大的顺序排队”是正确的贪心策略,能保证“获得奖赏最多的大臣其所获得的奖赏尽可能少”。
2、数据的组织,Person结构以及STL算法库排序函数的应用
得到上面的贪心策略之后,我们就可以搭建出本题算法的框架:
读入国王和所有大臣的左右手数字,并按各自左右手数字之积进行升序排序。
依此计算每一个大臣应得奖赏的数额,并统计出其中的最大值。
输出答案。
看上去事情已经非常简单了,但实际上只有第三步是真的简单,其他两步都不是那么简单的。我们先考虑第一步怎么做。
数据的组织方式很明确应该是顺序表,每个人(国王和大臣)有左手右手两个数字,显然用一个结构来组织这两个数字并把他们放入一个顺序表中是最合理的数据结构。所以我们可以先定义这样一个数据结构:
struct Person {
int a;
int b;
};
然后在 main() 函数中用一个 vector<Person> 来存放所有人,按顺序读入所有数据,组织成结构变量依序存放起来即可:
这样数据就被正确的读入了,按照输入数据格式,国王天然地会被存放在第一个元素。so easy!接下来就是不easy的部分了。说到排序,还不是太麻烦,因为我们当然是用 algorithm 库的 sort() 函数了。
按照前面的分析,我们这里的排序是以每个人左右手数字之积 \(a_i\cdot b_i\) 为关键字的,所以我们要么为 Person 结构重载小于运算,实现按两个成员变量之积比较大小,要么把这个比较运算做成一个单独的比较函数。像本题这样只用一种排序规则的情形通常重载运算符就好。
现在,我们可以完成整个算法的第一步了,读入数据,按照每个元素中两个成员变量的乘积进行升序排序。写完主体后在最后写上 Person 结构的 < 运算符重载函数,很简单,返回比较两个乘积的结果即可。按照题目中给出的数据取值范围,左右手数字之积不会超过108,还在 int 的取值范围之内,所以这里暂时还不需要用到高精算法。下面是这部分的完整代码:
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
struct Person {
int a;
int b;
bool operator<(const Person p) const;
};
int main()
{
vector<Person> persons;
int n;
cin >> n;
for (int i = 0; i <= n; ++i) {
Person p;
cin >> p.a >> p.b;
persons.push_back(p);
}
sort(persons.begin()+1, persons.end());
return 0;
}
bool Person::operator<(const Person p) const { return a * b < p.a * p.b; }
小技巧
这里我们推荐一种好的代码风格:当需要编写大量自定义函数(成员函数)的时候,先在 main() 函数之前写好所有自定义函数的原型,暂时先不要去写函数的定义。我们先集中精力把算法的主程序写完,然后再去写自定义函数。自定义函数的函数体全部放在 main() 函数之后,整个程序各部分的先后顺序依次为:引入库、命名空间、全局变量(常量)、自定义数据结构、自定义函数原型、 main() 函数、自定义函数。这样 main() 函数中的算法主程序和数据结构、函数原型这些部分能尽量贴近,易于阅读也方便编程。
再接下来就是真正麻烦的第二步了,统计每个大臣应得奖赏的最大值。在一系列整数中统计最大值难道不是quite easy的事情吗?No!这个题目里的奖赏数是超大的,一定会用到高精度,这就是麻烦所在。
3、简化版高精度算法
题目的数据取值范围显示,大臣人数最大可能有1000人,左右手的数字最大可能为9999。在计算大臣应得奖赏时,数字显然会超过C++内置整数中最大的 unsigned long long 型的取值范围。这是一个坏消息:必须使用高精度算法。
不过只要善于分析,就能找到一些好消息。仔细观察上述取值范围和奖赏数计算方法,我们可以发现所有的数据不超过10000,连乘的时候其中一个乘数必是一万以内的正整数,整个算法只用到乘、除和比较三种运算。这就给我们要写的高精度算法带来了诸多便利:
恰好可以采用万进制;
不需要实现高精度的输入流重载,只需实现输出即可;
不需要实现赋值运算,构造器也只需要能用
int型初始值构造即可,而且初始值都在10000以内,所以一定是恰为1节,构造器代码会非常简单;只需重载
*=, /, <三种运算;因为
*=运算的参数一定是10000以内的正整数,所以乘法可以直接将该参数从低到高依次乘到自身各节上去,然后按运算规则写数进位即可;因为
/运算的除数一定是10000以内的正整数,所以除法可以直接从高到低用各节除以除数,取数留余即可,使用的是int的除法和取余运算,不需要用高精度减法来模拟。
下面是完整的AC代码:
#include <iostream>
#include <iomanip>
#include <vector>
#include <algorithm>
using namespace std;
struct Person {
int a;
int b;
bool operator<(const Person p) const;
};
struct BigInt {
static const int _BASE = 10000;
vector<int> _s;
BigInt(int value);
BigInt &operator*=(int a);
BigInt operator/(int a) const;
bool operator<(const BigInt &a) const;
};
ostream &operator<<(ostream &os, const BigInt &bi);
int main()
{
vector<Person> persons;
int n;
cin >> n;
for (int i = 0; i <= n; ++i) {
Person p;
cin >> p.a >> p.b;
persons.push_back(p);
}
sort(persons.begin()+1, persons.end());
BigInt left(persons[0].a);
BigInt max(persons[0].a / persons[1].b);
for (int i = 2; i <= n; ++i) {
left *= persons[i-1].a;
BigInt current = left / persons[i].b;
if (max < current) max = current;
}
cout << max << endl;
return 0;
}
bool Person::operator<(const Person p) const { return a * b < p.a * p.b; }
BigInt::BigInt(int value) { _s.push_back(value); }
BigInt &BigInt::operator*=(int a)
{
int carry = 0;
for (int i = 0; i < _s.size(); ++i) {
_s[i] *= a;
_s[i] += carry;
carry = _s[i] / _BASE;
_s[i] %= _BASE;
}
if (carry) _s.push_back(carry);
return *this;
}
BigInt BigInt::operator/(int a) const
{
BigInt q(0);
q._s.resize(_s.size(), 0);
int part = 0, i = _s.size();
while (--i >= 0) {
part = part * _BASE + _s[i];
q._s[i] = part / a;
part %= a;
}
while (q._s.size() > 1 && q._s.back() == 0) q._s.pop_back();
return q;
}
bool BigInt::operator<(const BigInt &a) const
{
if (_s.size() != a._s.size()) return _s.size() < a._s.size();
for (int i = _s.size() - 1; i >= 0; --i)
if (_s[i] != a._s[i]) return _s[i] < a._s[i];
return false;
}
ostream &operator<<(ostream &os, const BigInt &bi)
{
int i = bi._s.size();
os << bi._s[--i];
while (--i >= 0)
os << right << setw(4) << setfill('0') << bi._s[i];
return os;
}
注解
BigInt 的输出流重载函数和 < 比较函数和前面几节已经讲解过的完全一样。请记住,同种数据类型的变量之间的赋值是不需要自己重载赋值运算来实现的,这种拷贝赋值是C++天生就会完成的任务。
算法主体程序中,left 变量保存到目前为止前面所有人左手上数字的乘积,max 变量保存的是到目前为止最大的奖赏数,统计最大值的循环体中的临时变量 current 是当前大臣应得的奖赏数。
最后再强调一下,一定要看懂 *= 和 / 这两个简化过的高精度乘除运算。

看,速度还是非常快的。